1. Prove or disprove: 9, 6, 5, 5, 3, 3, 2, 1, 1 are the vertex degrees of some graph.
Each edge contributes one degree to each of its two endpoints, therefore $\Sigma_{v \in V(G)}d(v)=2e(G)$, which supposed to be a even number. The sum of degrees is 9 + 6 + 5 + 5 + 3 + 3 + 2 + 1 + 1 = 35. Since 35 is an odd number, so it’s not a graph.
2. Prove or disprove that Petersen graph has girth 5.
- Petersen graph is a simple graph, so there is no 1-cycle and 2-cycle
- A 3-cycle require three pairwise-disjoint 2-sets, which cannot occur among 5
elements.
12, 34, 5? ====> cannot make it - A 4-cycle in the absence of 3-cycles would require nonadjacent vertices with two
common neighbors.
12, 34, 15, 34 ====> 34 repeats - Take an example, 12, 35, 24, 51, 34 yield a 5-cycle.
Therefore, Petersen graph has girth 5.
3. What is the chromatic number of the following graph?
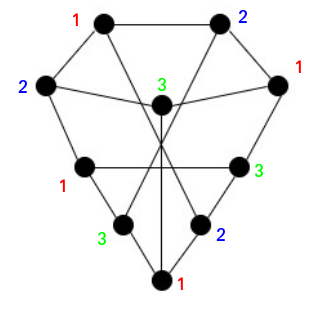
The chromatic number is 3.
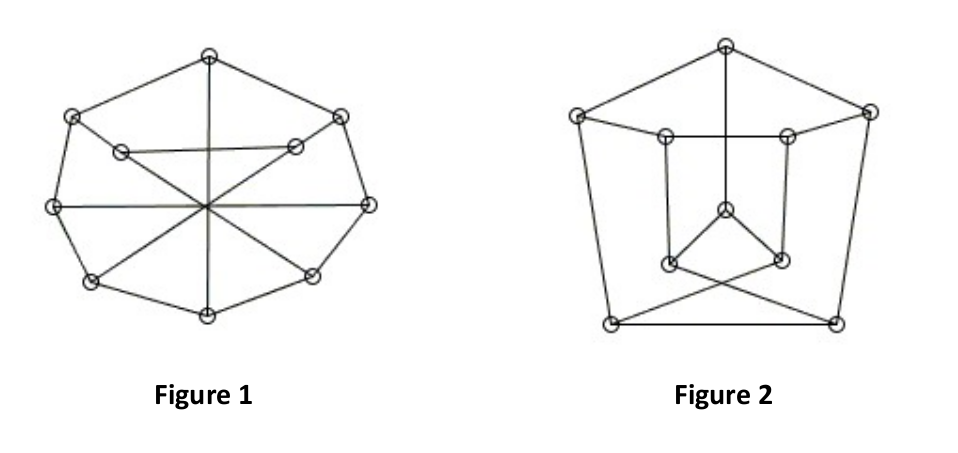
4. Is it isomorphism from Figure 1 to Figure 2?
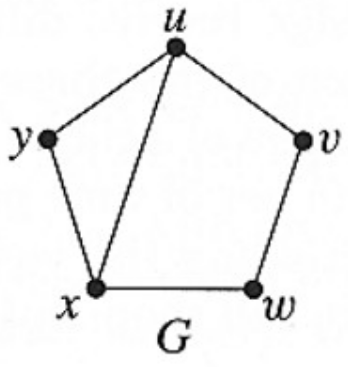
5. Please show the adjacency matrix and incidence matrix of the digraph $G$.
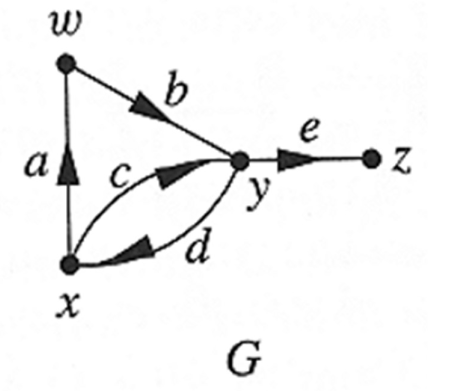
6. Please show the equivalence classes of the connection relation on $V(G)$.
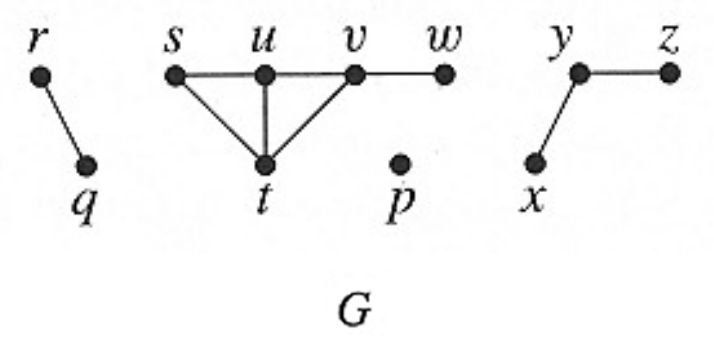
7. Draw the complement $\bar{G}$ of the simple graph $G$.