必要條件:
令 $G$ 為一個 bipartite,因為在 $G$ 中每走過一條邊,就會進入另一組 bipartition,所以要從某一點出發再走回該點,必定要走偶數次,故 $G$ 沒有 odd cycle。
充分條件:
令 $G$ 為無 odd cycle 的圖,並建構 $G$ 的 bipartite,從中選取一個 nontrivial component $H$,再從 $H$ 中選定 $u$ 點,令 $f(v)$ 為 $u$ 到 $H$ 中的任意點 $v$ 的最短路徑,然後我們畫分兩個集合:
\[X=\{v \in V(H):f(v)\ is\ even\}\\ Y=\{v \in V(H):f(v)\ is\ odd\}\]觀察發現 $X$、$Y$ 各自在 bipartite 的一個集合中,如下圖。
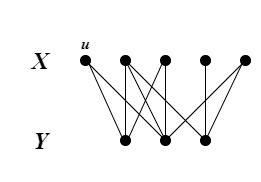
我們可以在 $X$ 或 $Y$ 集合中任找兩個點 $v$ 與 $v’$($v$ 與 $v’$ 必須同在 $X$ 或 $Y$ 集合),並新增一個邊連接 $vv’$,如此便完成一個 odd cycle,然而依據 bipartite 的定義,同一個 partition 的點之間不能有邊,$vv’$ 會直接破壞 bipartite:
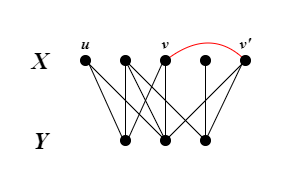
因此有 odd cycle 的圖必不為 bipartite。