Bloom Filter 在實作 key value storage 帶給我很大的效能優化,所以想特別做一份筆記紀錄,但是這個 bloom filter 是基於 jserv 老師在 dict 裡的實作,不是我原創的內容。
Bloom Filter 簡介
因為懶得自己措辭,所以以下簡介摘錄自 jserv 的上課教材 https://hackmd.io/@sysprog/2020-dict 以及維基百科
Bloom filter 利用 hash function,在不用走訪全部元素的前提,預測特定字串是否存於資料結構中。因此時間複雜度是 $O(1)$,而非傳統逐一尋訪的 $O(n)$ 。
- n-bits 的 table
- k 個 hash fucntion: $h_1$ 、 $h_2$ … $h_k$
- 每當要加入新字串 s 時,會將 s 透過這 k 個 hash function 各自轉換為 table index (範圍:
0到n - 1) ,所以有 k 個 hash function ,就該有 k 個 index ,然後將該table[index]上的 bit set - 下次若要檢查該字串 s 是否存在時,只需要再跑一次那 k 個 hash function ,並檢查是否所有的 k 個 bit 都是 set 即可
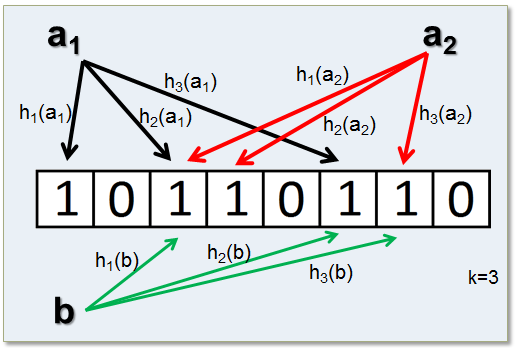
但這做法存在錯誤率,例如原本沒有在資料結構中的字串 s1 經過 hash 轉換後得出的 bit 的位置和另一個存在於資料結構中的字串 s2 經過 hash 之後的結果相同,如此一來,先前不存在的 s1 便會被認為存在,這就是 false positive (指進行實用測試後,測試結果有機會不能反映出真正的面貌或狀況)。
Bloom filter 一類手法的應用很常見。例如在社群網站 Facebook,在搜尋欄鍵入名字時,能夠在 20 億個註冊使用者 (2017 年統計資料) 中很快的找到結果,甚至是根據與使用者的關聯度排序。
延伸閱讀:
Bloom Filter 實作方式
首先,建立一個 n bits 的 table,並將每個 bit 初始化為 0。
我們將所有的字串構成的集合 (set) 表示為 $S = { x_1, x_2, x_3, … ,x_n}$,Bloom Filter 會使用 k 個不同的 hash function,每個 hash function 轉換後的範圍都是 0 到 n-1 (為了能夠對應上面建立的 n bits table)。而對每個 S 內的 element x~i~,都需要經過 k 個 hash function,一一轉換成 k 個 index。轉換過後,table 上的這 k 個 index 的值就必須設定為 1。
注意: 可能會有同一個 index 被多次設定為
1的狀況
Bloom Filter 這樣的機制,存在一定的錯誤率。若今天想要找一個字串 x 在不在 S 中,這樣的資料結構只能保證某個 $x_1$ 一定不在 S 中,但沒辦法 100% 確定某個 $x_2$ 一定在 S 中。因為會有誤判 (false positive) 的可能。
此外,資料只能夠新增,而不能夠刪除,試想今天有兩個字串 $x_1$, $x_2$ 經過某個 hash function $h_i$ 轉換後的結果 $h_i(x_1) = h_i(x_2)$,若今天要刪除 $x_1$ 而把 table 中 set 的 1 改為 0,豈不是連 $x_2$ 都受到影響?
Bloom Filter 錯誤率計算
首先假設我們的所有字串集合 S 裡面有 n 個字串, hash 總共有 k 個,Bloom Filter 的 table 總共 m bits。我們會判斷一個字串存在於 S 內,是看經過轉換後的每個 bits 都被 set 了,我們就會說可能這個字串在 S 內。但試想若是其實這個字串不在 S 內,但是其他的 a b c 等等字串經過轉換後的 index ,剛好涵蓋了我們的目標字串轉換後的 index,就造成了誤判這個字串在 S 內的情況。
如上述,Bloom Filter 存有錯誤機率,程式開發應顧及回報錯誤機率給使用者,以下分析錯誤率。
當我們把 S 內的所有字串,每一個由 k 個 hash 轉換成 index 並把 table[index] 設為 1,而全部轉完後, table 中某個 bits 仍然是 0 的機率是 $(1-\dfrac{1}{m})^{kn}$ 。
其中 $(1-\dfrac{1}{m})$ 是每次 hash 轉換後,table 的某個 bit 仍然是 0 的機率。因為我們把 hash 轉換後到每個 index (而這個 index 會被 set) 的機率視為相等 (每人 $\dfrac{1}{m}$),所以用 1 減掉即為不會被 set 的機率。我們總共需要做 kn 次 hash,所以就得到答案$(1-\dfrac{1}{m})^{kn}$。
由 $(1-\dfrac{1}{m})^{m}≈e^{-1}$ 特性,$(1-\dfrac{1}{m})^{kn}=((1-\dfrac{1}{m})^{m})^{\frac{kn}{m}}≈(e^{-1})^{\frac{kn}{m}}≈e^{-\frac{kn}{m}}$ 以上為全部的字串轉完後某個 bit 還沒有被 set 的機率。
因此誤判的機率等同於全部經由 k 個 hash 轉完後的 k bit 已經被其他人 set 的機率: 轉完後某個 bit 被 set 機率是: $1-e^{-\frac{kn}{m}}$,因此某 k bit 被 set 機率為: $(1-e^{-\frac{kn}{m}})^k$
延伸閱讀:
C++ 實作
以下原始碼也放在我的 github repo https://github.com/blueskyson/data-structure/tree/master/cpp/bloom-filter
bloom.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
typedef unsigned int (*hash_function)(const void *data);
struct hash_node {
hash_function func;
hash_node* next;
};
class BloomFilter {
public:
BloomFilter(unsigned size);
void add(void *data);
bool contains(void *data);
unsigned item_count();
unsigned hash_count();
double FPR();
~BloomFilter();
private:
unsigned char *table;
unsigned _size, _hash_count, _item_count;
hash_node *head;
void add_hash(hash_function f);
};
bloom.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include "bloom.h"
#include <cstring>
#include <cmath>
static unsigned int djb2(const void *_str)
{
const char *str = (const char *)_str;
unsigned int hash = 5381;
char c;
while ((c = *str++)) {
hash = ((hash << 5) + hash) + c;
}
return hash;
}
static unsigned int jenkins(const void *_str)
{
const char *key = (const char *)_str;
unsigned int hash = 0;
while (*key) {
hash += *key;
hash += (hash << 10);
hash ^= (hash >> 6);
key++;
}
hash += (hash << 3);
hash ^= (hash >> 11);
hash += (hash << 15);
return hash;
}
BloomFilter::BloomFilter(unsigned size) {
_size = size;
table = new unsigned char[size];
memset(table, 0, size);
_item_count = 0;
_hash_count = 0;
head = NULL;
add_hash(djb2);
add_hash(jenkins);
}
void BloomFilter::add_hash(hash_function f) {
hash_node *h = new hash_node;
h->func = f;
h->next = NULL;
_hash_count++;
if (head == NULL) {
head = h;
return;
}
hash_node *last = head;
while (last->next != NULL) {
last = last->next;
}
last->next = h;
}
void BloomFilter::add(void *data) {
hash_node *h = head;
_item_count++;
while (h) {
unsigned hash = h->func(data);
hash %= _size;
table[hash >> 3] |= 0x80 >> (hash & 7);
h = h->next;
}
}
bool BloomFilter::contains(void *data) {
hash_node *h = head;
while (h) {
unsigned hash = h->func(data);
hash %= _size;
if (!(table[hash >> 3] & (0x80 >> (hash & 7)))) {
return false;
}
h = h->next;
}
return true;
}
double BloomFilter::FPR() {
double p = (-1.0 * _hash_count * _item_count) / _size;
return pow(1 - exp(p), (double)_hash_count);
}
unsigned BloomFilter::item_count() {
return _item_count;
}
unsigned BloomFilter::hash_count() {
return _hash_count;
}
BloomFilter::~BloomFilter() {
while (head) {
hash_node *p = head;
head = head->next;
delete p;
}
delete[] table;
}
使用範例
example.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include "bloom.h"
#include <iostream>
using namespace std;
int main() {
cout << "Construct a bloom filter with 1024 bytes (8192 bits).\n"
<< "The bloom filter has 2 hash funtions: djb2, jenkins.\n"
<< endl;
BloomFilter bloom(1024);
cout << "Test if string \"hello\" is in the bloom filter. (1 => true, 0 => false)\n";
cout << bloom.contains((void*)"hello") << "\n"
<< endl;
cout << "Add string \"hello\" to the bloom filter\n" << endl;
bloom.add((void*)"hello");
cout << "Test if string \"hello\" is in the bloom filter again.\n";
cout << bloom.contains((void*)"hello") << "\n" << endl;
cout << "Add other 9 strings: a, b, c, d, aa, aaa, bbb, cc, ddd\n"
<< endl;
bloom.add((void*)"a");
bloom.add((void*)"b");
bloom.add((void*)"c");
bloom.add((void*)"d");
bloom.add((void*)"aa");
bloom.add((void*)"aaa");
bloom.add((void*)"bbb");
bloom.add((void*)"cc");
bloom.add((void*)"ddd");
cout << "Test if string \"aaa\" is in the bloom filter.\n";
cout << bloom.contains((void*)"aaa") << "\n" << endl;
cout << "Test if string \"xyz\" is in the bloom filter.\n";
cout << bloom.contains((void*)"xyz") << "\n" << endl;
cout << "False positive rate of the bloom filter: " << bloom.FPR() << endl;
cout << "The bloom filter contins " << bloom.item_count() << " items.\n";
return 0;
}
執行
$ g++ example.cpp bloom.cpp -o a
$ ./a
Construct a bloom filter with 1024 bytes (8192 bits).
The bloom filter has 2 hash funtions: djb2, jenkins.
Test if string "hello" is in the bloom filter. (1 => true, 0 => false)
0
Add string "hello" to the bloom filter
Test if string "hello" is in the bloom filter again.
1
Add other 9 strings: a, b, c, d, aa, aaa, bbb, cc, ddd
Test if string "aaa" is in the bloom filter.
1
Test if string "xyz" is in the bloom filter.
0
False positive rate of the bloom filter: 0.000374103