The conversion of positional notation is quite important in computer science since the data are stored as binary signals in disks and memories. We must convert them into decimal so as to make use of them.
Binary to Decimal Example
Convert binary number $ 101011 $ into decimal. First of all, every digit corresponds with an exponentiation of $ 2 $, that is:
$ 2^5=32,\ \ \ \ 2^4=16,\ \ \ \ 2^3=8,\ \ \ \ 2^2=4,\ \ \ \ 2^1=2,\ \ \ \ 2^0=1 $
Multiply each digit by its corresponding place value
$ 1×32 + 0×16 + 1×8 + 0×4 + 1×2 + 1×1 = 43 $
| binary | 1 | 0 | 1 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| decimal | 32 | 0 | 8 | 0 | 2 | 1 |
So $ (101011) _{2} = (43) _{10} $
Decimal to Binary Example
From decimal to binary can be considered the opposite steps:
$ 43 = 1×32 + 0×16 + 1×8 + 0×4 + 1×2 + 1×1 $
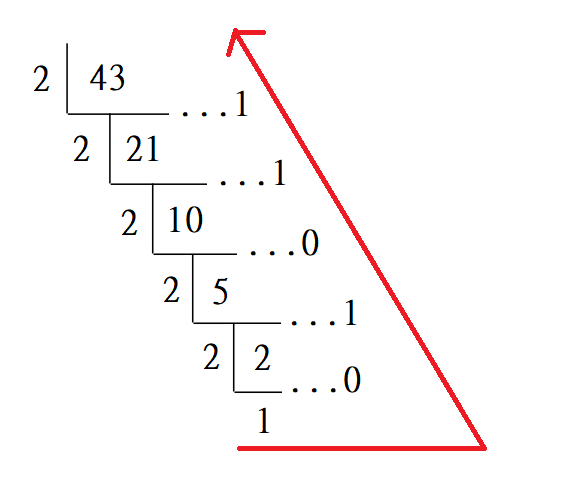
Here is a faster way called short division for doing this conversion, a number after ellipsis is the remainder of number in the short division divided by $ 2 $:
By assembling all remainders, we get $ (43) _{10} = (101011) _{2} $
Other Bases Conversion
Take decimal number $ 60 $ as example, we want to convert it from decimal to base-7. First, use the exponentiation way:
$ 7^2=49,\ \ \ \ 7^1=7,\ \ \ \ 7^0=1 $
Multiply each digit by its corresponding place value
$ 60 = 1×49 + 1×7 + 4×1 $
| base-7 | 1 | 1 | 4 |
|---|---|---|---|
| decimal | 49 | 7 | 4 |
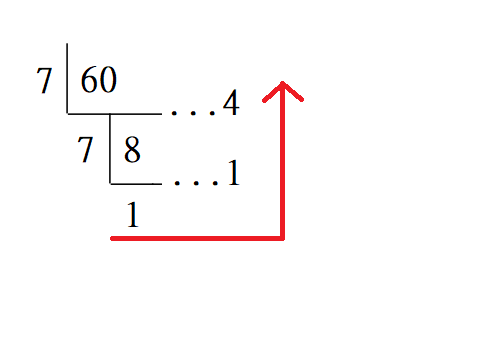
So $ (60) _{10} = (114) _{7} $
Then we try short division, the result is still correct: