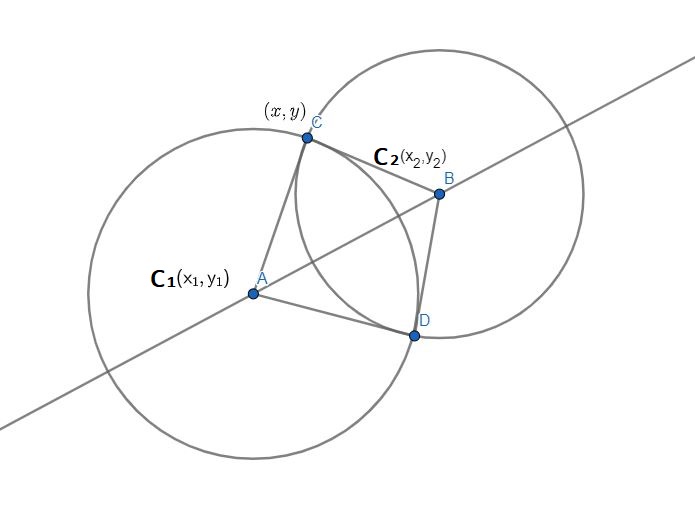
This post is for solving the intersections of two circles.
Suppose the radius of $ C_1 $ is $ r_1 $, and the radius of $ C_2 $ is $ r_2 $.
Let $ θ $ be the angel between $ \overline{A C} $ and horizontal line. Our strategy is find the value of $ cos\ θ $ and use it to calculate $ (x, y) $.
$ x = r_1 * cos θ + x_1 \ \ \ \ …(1)\\ y = r_1 * sin θ + y_1 \ \ \ \ …(2)\\ (x - x_2)^2 + (y - y_2)^2 = r_2^2 \ \ \ \ …(3)\\ $
Substitute (1) and (2) into (3), we get:
$ (r_1 * cos θ + x_1 - x_2)^2 + (r_1 * sin θ + y_1 - y_2)^2 = r_2^2\\ $
After expansion and simplification, the equation above becomes:
$ r_1^2 * (sin^2 θ + cos^2 θ) + 2r_1 * (x_1 - x_2) * cos θ + 2r_1 * (y_1 - y_2) * sin θ\\ = r_2^2 - (x_1 - x_2)^2 - (y_1 - y_2)^2 \ \ \ \ …(4)\\ $
Let:
$ a = 2r_1 * (x_1 - x_2)\\ b = 2r_1 * (y_1 - y_2)\\ c = r_2^2 - r_1^2 - (x_1 - x_2)^2 - (y_1 - y_2)^2\\ $
Substitute $ a, b, c $ into (4), the equation becomes:
$ a* cos θ + b *sin θ = c\\ $
Substitute $ sin θ $ into $\sqrt[]{1 - cos^2 θ} $ and rearrange the equation:
$ a * cos θ - c = - \sqrt[]{1 - cos^2 θ} \\ a^2 * cos^2 θ - 2ac * cos θ + c^2 = b^2 - b^2 * cos^2 θ\\ (a^2 + b^2) * cos^2 θ - 2ac * cos θ + (c^2 - b^2) = 0\\ $
Let:
$ p = a^2 + b^2\\ q = -2ac\\ r = c^2 - b^2\\ $
Finally we get $ cos θ = \frac{-q ± \sqrt[]{q^2 - 4pr}}{2p} $
There are two $ cos θ $ values, we need to verify which one is the real solution by substituting them into (1) and (2).